Quantum physics, also known as quantum mechanics or quantum theory, is a fundamental branch of physics that describes the behavior of matter and energy at the smallest scales, such as atoms and subatomic particles. It challenges the classical physics view by introducing concepts like wave-particle duality, quantization, and uncertainty, which are essential for understanding the micro-world.

Historical Background

The development of quantum physics began in the early 20th century as scientists tried to explain phenomena that classical physics could not, such as blackbody radiation and the photoelectric effect. Key figures in the development of quantum theory include Max Planck, Albert Einstein, Niels Bohr, Werner Heisenberg, and Erwin Schrödinger.

Key Milestones:

• Max Planck (1900): Introduced the concept of quantization, proposing that energy is emitted in discrete units called “quanta.”
• Albert Einstein (1905): Explained the photoelectric effect using quantum concepts, showing that light can be thought of as particles (photons) as well as waves.
• Niels Bohr (1913): Developed the Bohr model of the atom, incorporating quantized orbits for electrons.
• Werner Heisenberg (1927): Formulated the Uncertainty Principle, stating that certain pairs of physical properties cannot be simultaneously known with arbitrary precision.
• Erwin Schrödinger (1926): Developed wave mechanics, introducing the Schrödinger equation to describe how quantum states evolve over time.

Fundamental Principles of Quantum Physics

1. Wave-Particle Duality

Particles at the quantum level, such as electrons and photons, exhibit both wave-like and particle-like properties. This duality is exemplified in experiments like the double-slit experiment, where particles create an interference pattern characteristic of waves, yet are detected as discrete particles.

2. Quantization

Energy levels in atoms are quantized, meaning they can only take on certain discrete values. This is why electrons in an atom can only occupy specific orbitals and why atoms emit or absorb energy in discrete packets or photons.

3. Uncertainty Principle

Formulated by Heisenberg, this principle states that certain pairs of properties, like position and momentum, cannot both be precisely measured simultaneously. The more accurately one property is known, the less accurately the other can be known.

4. Superposition

Quantum systems can exist in multiple states simultaneously until a measurement is made. For example, a quantum bit (qubit) can be in a state of 0, 1, or any superposition of these states, enabling parallel computation.

5. Entanglement

Entangled particles are interconnected such that the state of one particle instantaneously influences the state of another, regardless of distance. This phenomenon has been experimentally verified and is a key resource for quantum computing and quantum communication.

Quantum Mechanics Formalism

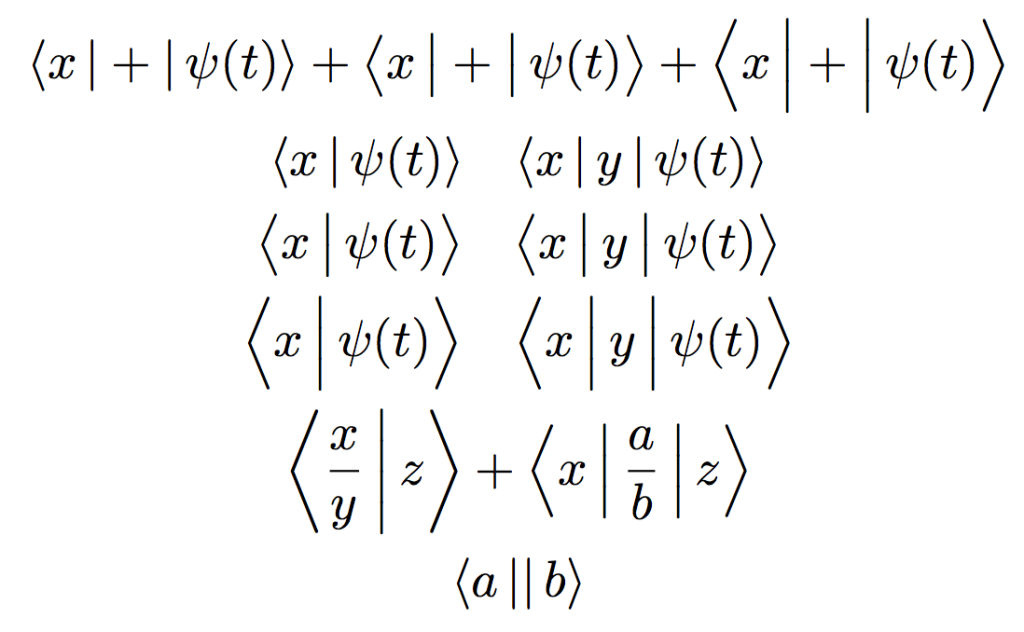
1. Wave Functions and the Schrödinger Equation

The wave function, represented by the Greek letter ψ (psi), describes the quantum state of a particle or system. The square of the wave function’s amplitude gives the probability of finding a particle in a particular state. The Schrödinger equation governs how wave functions evolve over time:

iℏ∂∂tψ(x,t)=H^ψ(x,t)i\hbar \frac{\partial}{\partial t}\psi(x, t) = \hat{H}\psi(x, t)iℏ∂t∂​ψ(x,t)=H^ψ(x,t)

where ℏ\hbarℏ is the reduced Planck’s constant, ψ(x,t)\psi(x, t)ψ(x,t) is the wave function, and H^\hat{H}H^ is the Hamiltonian operator representing the total energy of the system.

2. Operators and Observables

In quantum mechanics, physical quantities are represented by operators, mathematical entities that act on wave functions to extract information about the system. For example, the position operator x^\hat{x}x^ and momentum operator p^\hat{p}p^​ are used to obtain the position and momentum of a particle, respectively.

3. Eigenvalues and Eigenstates

An observable measurement in a quantum system results in an eigenvalue, with the system being in the corresponding eigenstate. The eigenvalue equation is given by:

A^ψ=aψ\hat{A}\psi = a\psiA^ψ=aψ

where A^\hat{A}A^ is the operator, aaa is the eigenvalue, and ψ\psiψ is the eigenstate.

Quantum Physics Applications

Quantum physics has led to groundbreaking technological advancements and applications in various fields:-

1. Quantum Computing

Quantum computers leverage quantum bits (qubits) to perform computations exponentially faster than classical computers for certain problems. Algorithms like Shor’s for factorization and Grover’s for searching databases highlight the potential of quantum computing.

2. Quantum Cryptography

Quantum cryptography uses the principles of quantum mechanics to secure communication. Quantum key distribution (QKD) allows two parties to generate a shared secret key with security guaranteed by the laws of physics.

3. Quantum Sensors and Metrology

Quantum sensors exploit quantum effects to achieve unprecedented precision in measuring physical quantities like time, gravity, and magnetic fields. Examples include atomic clocks and gravitational wave detectors.

4. Quantum Teleportation and Communication

Quantum teleportation transfers the quantum state of a particle to another particle at a distant location, using entanglement and classical communication. This phenomenon is crucial for future quantum networks and the development of a quantum internet.

Challenges and Future Directions

Despite its successes, quantum physics presents several challenges and opportunities for future research:-

• Interpretational Issues: The interpretation of quantum mechanics remains a topic of debate, with various interpretations like Copenhagen, many worlds, and pilot waves offering different perspectives on the nature of reality.
• Scalability: Building large-scale quantum systems, such as quantum computers, that can operate with low error rates and high fidelity.
• Quantum Gravity: Developing a consistent theory of quantum gravity that unifies general relativity and quantum mechanics remains one of the biggest challenges in theoretical physics.

The future of quantum physics holds promise for further advancements in technology and a deeper understanding of the fundamental nature of the universe.

Thanks,